ROL’s key design feature is an abstract linear algebra interface, through the Vector class, which enables the use of any ROL algorithm with any data type, such as the C++ std::vector, MPI-parallel data structures (e.g., Epetra, Tpetra, PETSc, HYPRE vectors), GPU data structures (e.g., Kokkos, ArrayFire), etc.
Additionally, the Vector class allows the user to define a custom inner product (dot product) for the vector space, and to define mappings between the vector space and its dual space. For optimization problems defined in function space, e.g., problems governed by differential equations, ROL’s algorithms can use the custom inner product to achieve iteration complexity that is independent of the size of the function discretization. This feature, sometimes referred to as mesh independence, allows ROL to solve optimization problems with billions of variables.
Finally, all ROL algorithms are matrix-free, and rely on user-defined applications of linear and nonlinear operators to vectors and, where applicable, applications of their inverses. These operations comprise ROL’s functional interface. A special middleware for simulation-constrained optimization, called SimOpt, is also provided. Once the vectors and functions are defined, the user defines an optimization Problem and solves it using an optimization Solver, which are part of the algorithmic interface.
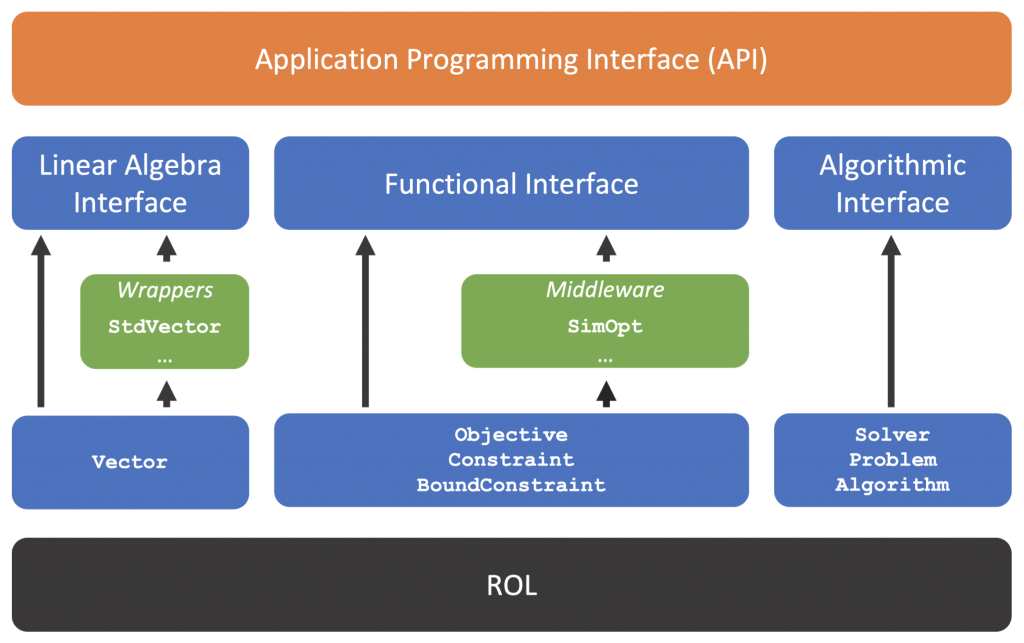
The design of ROL’s linear algebra interface is inspired by the following projects:
Hilbert Class Library
M.S. Gockenbach, W.W. Symes (1996) Hilbert class library: A library of abstract C++ classes for optimization and inversion, Computers & Mathematics with Applications 32(6), 1-13.
Vector Reduction/Transformation Operators (RTOp) and Thyra (Trilinos)
R.A. Bartlett, B.G. van Bloemen Waanders, M.A. Heroux (2004) Vector reduction/transformation operators. ACM Transactions on Mathematical Software 30(1), 62-85.
Rice Vector Library
A.D. Padula, S.D. Scott, W.W. Symes (2009) A software framework for abstract expression of coordinate-free linear algebra and optimization algorithms. ACM Transactions on Mathematical Software 36(2), 1-36.
ROL’s functional interface and the SimOpt middleware are motivated by the following:
Interface between Optimization and Application
M. Heinkenschloss, L.N. Vicente (1999) An interface between optimization and application for the numerical solution of optimal control problems. ACM Transactions on Mathematical Software 25(2), 157-190.
MOOCHO
R.A. Bartlett (2009) Mathematical and High-Level Overview of MOOCHO: The Multifunctional Object-Oriented arCHitecture for Optimization. Technical report SAND2009-3969, Sandia National Laboratories, June 2009.
ROL features a large collection of well-established algorithms for smooth optimization as well as several novel algorithms developed by the ROL team. ROL categorizes optimization problems into 4 basic types, based on the presence of certain constraints: Type U (unconstrained), Type B (bound constraints), Type E (equality constraints) and Type G (general constraints). Additionally, each problem type can include linear constraints, which ROL can reduce/eliminate algorithmically. Here is a sample mapping of problem types and algorithms:

Here are some algorithms for smooth optimization developed by the ROL team:
H. Antil, D.P. Kouri, D. Ridzal (2023) ALESQP: An Augmented Lagrangian Equality-Constrained SQP Method for Optimization with General Constraints, SIAM J. Optimization 33(1), 237-266.
D.P. Kouri (2022) A matrix-free trust-region Newton algorithm for convex-constrained optimization, Optimization Letters 16, 983-997.
M. Heinkenschloss, D. Ridzal (2014) A Matrix-Free Trust-Region SQP Method for Equality Constrained Optimization, SIAM J. Optimization 24(3), 1507-1541.
ROL contains specialized interfaces and algorithms for stochastic optimization. Optimization problems with stochastic and uncertain problem data pose challenges in problem formulation and efficient numerical solution methods. ROL’s interface for stochastic optimization enables the use of numerous modern risk measures, probabilistic functions and robust problem formulations. To approximate risk-averse problems, ROL includes sampled-based approaches such as sample average approximation, stochastic approximation, and adaptive sparse-grid quadrature. ROL also includes specialized algorithms such as progressive hedging and the primal dual risk minimization algorithm. For more information on these methods see:
D.P. Kouri, M. Heinkenschloss, D. Ridzal, B.G. van Bloemen Waanders (2013). A Trust-Region Algorithm with Adaptive Stochastic Collocation for PDE Optimization under Uncertainty, SIAM J. Scientific Computing. 35 (4), A1847-A1879.
D.P. Kouri, M. Heinkenschloss, D. Ridzal, B.G. van Bloemen Waanders (2014). Inexact Objective Function Evaluations in a Trust-Region Algorithm for PDE-Constrained Optimization under Uncertainty, SIAM J. Scientific Computing. 36 (6), A3011-A3029.
DP Kouri, TM Surowiec (2016). Risk-averse PDE-constrained optimization using the conditional value-at-risk, SIAM Journal on Optimization. 26 (1), 365-396
D.P. Kouri, T.M. Surowiec (2020). Epi-Regularization of Risk Measures, Mathematics of Operations Research. 45 (2), 774-795.
D.P. Kouri, T.M. Surowiec (2022). A Primal-Dual Algorithm for Risk Minimization, Mathematical Programming, 193, 337–363.
ROL also deploys novel algorithms for nonsmooth optimization developed by the team as well as several standard nonsmooth methods. The ROL categorization is Type P (proximable), which considers regularized functions composed of a nonconvex but smooth $$J(x)$$ and a convex but nonsmooth $$\phi(x)$$ for $$x$$ in Hilbert space. Function and derivative information for $$J(x)$$ may be inexact. The nonsmooth function $$\phi(x)$$ must be proximable.
| Type P Proximable |
|---|
| $$ \begin{align} \min_{x\in X} &\;\; J(x) + \phi(x) \end{align} $$ |
| Methods: $$\bullet$$ inexact nonsmooth trust-region globalization, with subsolver options. $$\bullet$$ proximal gradient, spectral proximal gradient, iPiano, inexact Newton, and inexact quasi-Newton. |
R. J. Baraldi, D. P. Kouri (2022) A proximal trust-region method for nonsmooth optimization with inexact function and gradient evaluations, Math Programming 201, 559–598.
ROL controls inexact function evaluations and exploits adaptive computations and multi-fidelity models through its trust-region methods. Several of these methods have been pioneered by the ROL team. Their implementations typically require some knowledge of error in the computations, i.e., an “error estimate.” For a comprehensive overview of problem formulations, algorithms with error control, and their ROL implementations, see:
D.P. Kouri, D. Ridzal (2018) Inexact Trust-Region Methods for PDE-Constrained Optimization. In: Antil, H., Kouri, D.P., Lacasse, MD., Ridzal, D. (eds) Frontiers in PDE-Constrained Optimization. The IMA Volumes in Mathematics and its Applications 163, 83-121. Springer, New York.
Related references:
M.J. Zahr, K.T. Carlberg, D.P. Kouri (2019) An Efficient, Globally Convergent Method for Optimization Under Uncertainty Using Adaptive Model Reduction and Sparse Grids, SIAM/ASA J. Uncertainty Quantification 7(3), 877-912.
M. Heinkenschloss, D. Ridzal (2014) A Matrix-Free Trust-Region SQP Method for Equality Constrained Optimization, SIAM J. Optimization 24(3), 1507-1541.
D.P. Kouri, M. Heinkenschloss, D. Ridzal, B.G. van Bloemen Waanders (2014) Inexact Objective Function Evaluations in a Trust-Region Algorithm for PDE-Constrained Optimization under Uncertainty, SIAM J. Scientific Computing 36(6), A3011-A3029.
D.P. Kouri, M. Heinkenschloss, D. Ridzal, B.G. van Bloemen Waanders (2013), A Trust-Region Algorithm with Adaptive Stochastic Collocation for PDE Optimization under Uncertainty, SIAM J. Scientific Computing 35(4), A1847-A1879.
To build and optimize models based on partial differential equations (PDEs), ROL offers an application development kit, called PDE-OPT. PDE-OPT is based on a modular, object-oriented design, with three fundamental layers: local computations, global computations, and interface to ROL (including SimOpt, Problem and Solver). The PDE-OPT figure illustrates the layers and the individual modules within them. We emphasize that the users need only implement the PDE and QoI virtual classes in the local computation layer of PDE-OPT. In finite element methods for PDEs, the local computations are, in essence, the evaluations of weak forms on individual mesh elements (mesh cells).
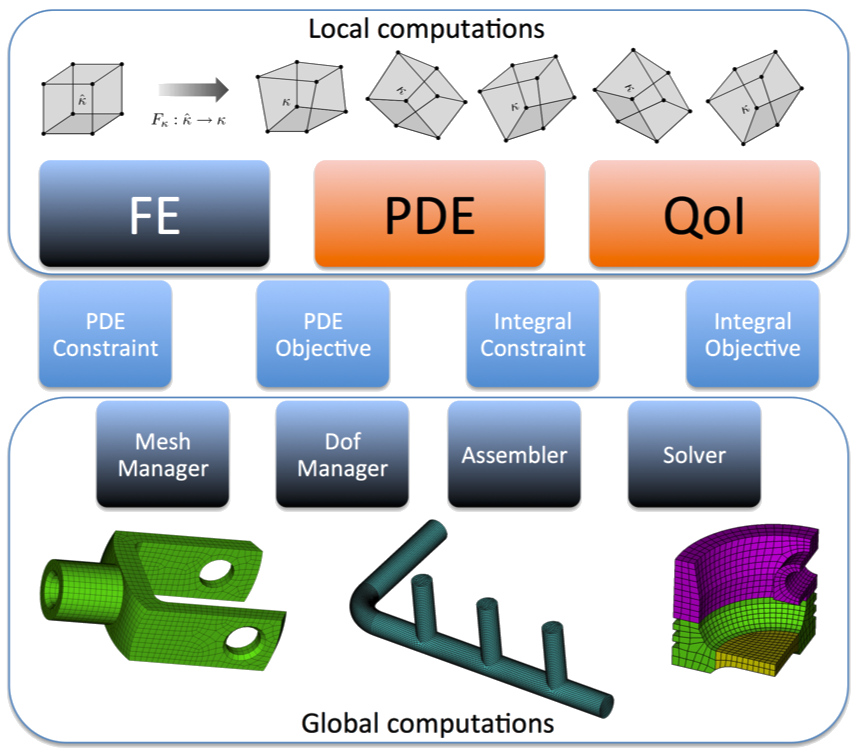
Components of the PDE-OPT Application Development Kit (ADK). The user implements the
PDE and QoI abstractions, see the orange modules. Other modules provide computational services without user intervention. Additionally, user customizations of the service modules are possible. Meshes courtesy of Cubit, https://cubit.sandia.gov.Local computations: The FE module provides definitions of finite element basis functions, geometric cell operations (mappings to reference cells, computation of cell volumes, tangents, normals, Jacobians, etc.) and local (cell-wise) numerical integration routines, through the Intrepid package from the Trilinos project. Based on the FE module the user implements local PDE residual equations and their derivatives by following the interface defined in the PDE class. For multiphysics problems, we follow a fully coupled approach where all solution fields are available in the PDE residual computation. Additionally, to specify objective functions, quantities of interest and their derivatives must be defined through the QoI interface. We note that the user can compute derivatives analytically, or obtain them using automatic differentiation tools from the Sacado package.
Global computations: The MeshManager module provides basic mesh generation services, as well as the numbering of mesh entities (vertices, edges, faces and volumes). The DofManager module is used to assign computational degrees of freedom to mesh entities. It enables the use of an arbitrary number of simulation, control, and design fields based on a variety of finite element discretizations, on 1D, 2D and 3D computational meshes. This capability simplifies the coupling of physics in the optimization context. The Assembler module combines global degree-of-freedom information with locally computed quantities (residuals, Jacobians, etc.), and populates global shared, distributed or hybrid data structures that are used to solve linear systems. This module relies on the Tpetra linear algebra package from the Trilinos project. The Solver module is used to solve linear systems built by the Assembler module, and utilizes the Belos, MueLu and Amesos2 packages from Trilinos for iterative and direct linear solvers and preconditioners.
Interface to ROL: To solve optimization problems, PDE-OPT interfaces the multiphysics components with the SimOpt programming interface from ROL. This “glue code” is contained in the PDE Constraint, PDE Objective, Integral Constraint and Integral Objective modules. The SimOpt interface enables a streamlined and efficient solution and verification of simulation-constrained optimization problems. Additional SimOpt infrastructure allows the user to easily extend their implementations of deterministic simulation-constrained optimization problems to include random simulation variables. These “stochastic” SimOpt implementations can be paired with a variety of risk measures available in ROL, enabling efficient risk-aware optimization.
Here is a listing of the physics modules implemented in PDE-OPT. Each module solves optimization problems governed by the given partial differential equations.
| Physics module | Equations |
| Convective heat transfer | Convection diffusion |
| Radiative heat transfer | Stefan Boltzmann |
| Semiconductor modeling | Poisson Boltzmann |
| Structural dynamics | Linear elasticity |
| Incompressible flow | Navier Stokes |
| Porous flow | Darcy |
| Naturally convected flow | Boussinesq |
| Superconductivity | Ginzburg Landau |
| Acoustics | Helmholtz |